|
论文导读:可以满足实时仿真要求。由于尾桨只有总距操纵。直升机的横向姿态要发生变化。
关键词:直升机,仿真,动态入流,操纵
直升机飞行仿真技术的应用,可以降低飞行员训练成本,帮助开发直升机飞控系统,开展直升机总体布局研究。飞行仿真技术的关键是要有一个可信的、实时的直升机飞行动力学模型。直升机是一个复杂的非线性系统,存在着较强的运动耦合、气动耦合、惯性耦合,其运动方程是一个大规模的非线性方程组,不仅求解难度大,而且不适于仿真计算,尤其不能满足实时仿真的要求。为满足实时仿真对飞行动力学模型的要求,本文提出一种相对复杂的工程化模型,该模型可有效缩短计算时间。
1适于实时仿真的直升机飞行动力学模型
1.1 全机欧拉方程
仿真用到的全机欧拉方程为:
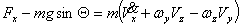
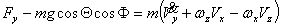
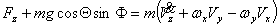 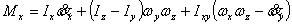 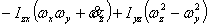
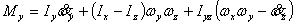 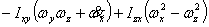
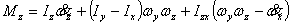 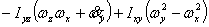
上式中,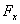 、 、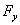 、 、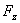 、 、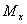 、 、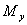 、 、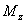 为作用在直升机上的外力(不含重力)的合力在机体坐标系上的投影。这些力和力矩包括旋翼、机身、平尾和尾桨的气动力和力矩。由旋翼、尾桨空气动力学方程和挥舞运动方程计算得到[1]。 为作用在直升机上的外力(不含重力)的合力在机体坐标系上的投影。这些力和力矩包括旋翼、机身、平尾和尾桨的气动力和力矩。由旋翼、尾桨空气动力学方程和挥舞运动方程计算得到[1]。
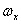 、 、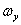 、 、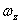 是直升机绕重心转动的角速度矢量在机体坐标系上的投影, 是直升机绕重心转动的角速度矢量在机体坐标系上的投影,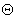 、 、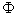 、 、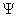 为机体俯仰角和侧倾角。 为机体俯仰角和侧倾角。
在已知飞行状态和气动力、气动力矩前提下,欧拉方程中有九个未知量,{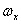 , ,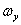 , ,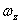 ; ;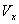 , ,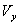 , ,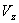 ; ;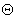 , ,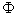 , ,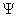 },为保证方程封闭,需加入姿态角及其变化量求解,经过整理,完整的待解方程如下: },为保证方程封闭,需加入姿态角及其变化量求解,经过整理,完整的待解方程如下:
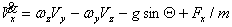 | 