|
论文导读:在这种情况下通过数据拟合方法对已获得数据进行分析。而是后来插值获得。
关键词:数据拟合,插值
1 引言
在进行航空发动机关键部件寿命计算时,需处理材料持久强度实验数据,分析材料力学性能。经常由于实验条件限制或其他原因,不能获得详细数据,而这些数据恰恰是进行寿命计算所必需的。在这种情况下通过数据拟合方法对已获得数据进行分析,在误差允许范围内可得到材料的近似特性。
最小二乘法是工程上经常应用的数据拟合方法,根据实验数据特点现用其对一组某航空材料的持久强度数据进行拟合,分析结果,证明其可靠性。
2 实验数据及拟合分析
2.1 实验数据及分析
持久应力-寿命曲线如图1,近似为一直线族。给出实验数据如表1,表中带下划直线数据为外推数据。
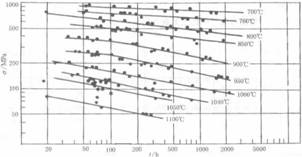
图1 持久应力-寿命曲线
对比图1和表1,显然表中数据并非原始数据。表1中数据散点图如图2,其线形并非直线。对表1中数据在双对数坐标系上观察其散点图,发现其近似为一直线,如图3。由此假设持久应力-寿命公式:
 (1) (1)
上式两边取对数,并整理后得到
 (2) (2)
幂函数的S-T曲线假想公式在双对数坐标系上为一直线。
| θ℃ |
σ 50 |
σ 100 |
σ 200 |
σ 300 |
σ 500 |
σ1000 |
σ2000 |
| 700 |
912 |
885 |
858 |
843 |
825 |
802 |
779 |
| 750 |
794 |
758 |
722 |
701 |
676 |
642 |
612 |
| 760 |
776 |
741 |
705 |
683 |
658 |
626 |
593 |
| 800 |
669 |
618 |
570 |
544 |
515 |
479 |
443 |
| 850 |
529 |
494 |
447 |
422 |
392 |
353 |
321 |
| 900 |
379 |
362 |
316 |
293 |
266 |
232 |
203 |
| 950 |
263 |
250 |
213 |
194 |
173 |
147 |
125 |
| 1000 |
181 |
161 |
139 |
127 |
114 |
98 |
84 |
| 1040 |
138 |
115 |
100 |
91 |
82 |
71 |
62 |
| 1050 |
114 |
97 |
83 |
76 |
68 |
60 |
52 |
| 1100 |
66 |
56 |
49 |
45 |
40 |
35 |
30 |
表1 持久强度数据
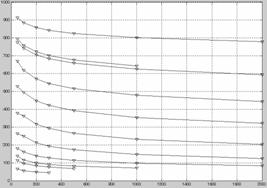
图2 持久强度数据散点图
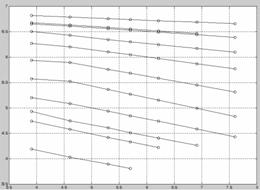
图3 双对数坐标系下持久强度数据散点图
因此采用最小二乘法【1】基于MATlab【2】对其进行线性拟合,得到回归方程。最小二乘法建立的偏差平方和:
 (3) (3)
应选择a,b使Q值最小,即Q对a,b的偏导数为0,根据表1已知应力、寿命,由偏导数方程组:
 (4) (4)
由此方程组得到a,b值,如表2。
| 温度 |
700 |
750 |
760 |
800 |
850 |
900 |
| a |
6.9819 |
6.9566 |
6.9432 |
6.9384 |
6.8298 |
6.6734 |
| b |
-0.0427 |
-0.0710 |
-0.0731 |
-0.1114 |
-0.1386 |
-0.1766 |
| 温度 |
950 |
1000 |
1040 |
1050 |
1100 |
|
| a |
6.4528 |
6.0402 |
5.7707 |
5.6103 |
5.0115 |
|
| b |
-0.2106 |
-0.2105 |
-0.2196 |
-0.2243 |
-0.2117 |
|
表2 各温度下回归方程 a, b值
从而确定各温度下回归方程组(2)。回归方程在一定程度上揭示了两个相关变量 , ,  之间的内在规律,在数学上用相关系数r表示两个变量线性关系的密切程度。论文发表。 之间的内在规律,在数学上用相关系数r表示两个变量线性关系的密切程度。论文发表。
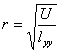
其中U为回归平方和, 为 为 的离差平方和。r的绝对值越接近1,说明两个变量关系越接近线性关系,拟合程度越好。论文发表。 的离差平方和。r的绝对值越接近1,说明两个变量关系越接近线性关系,拟合程度越好。论文发表。
将表1中数据(不含外推数据)带入回归方程组(2)既可得到拟合直线方程。论文发表。拟合结果在双对数坐标系上与散点图比较如图4。可见实验数据点非常接近拟合曲线。
计算得到不同试验温度下拟合直线的相关性系数如表3,拟合直线与散点图相关性系数非常接近1,表明用最小二乘法对此数据进行线性拟合是恰当的。但考虑到工程实际以及实验随机性,由此推断表1提供的实验数据并非原始数据,而是后来插值获得。
| 温度 |
700 |
750 |
760 |
800 |
850 |
900 |
| 相关 系数 |
- 0.9999 |
- 0.9998 |
- 0.9998 |
- 0.9998 |
- 0.9986 |
- 0.9936 |
| 温度 |
950 |
1000 |
1040 |
1050 |
1100 |
|
| 相关 系数 |
- 0.9929 |
- 0.9992 |
- 0.9990 |
- 0.9999 |
- 0.999 |
|
表3 拟合结果与散点图的相关系数
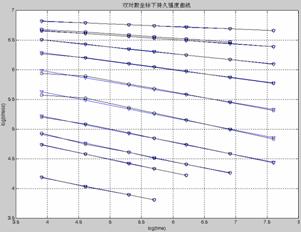
图4 双对数坐标系拟合结果与散点图比较
(三角符号为拟合直线,圆圈符号为散点图)
2.2 插值获得未知温度下的持久强度曲线
根据以上获得的回归方程对表1中未知数据进行外推计算,补充数据为表中带波浪线数据。由于实验条件或其他限制,不可能得到全部温度下材料的持久强度,拟合的目的就是对未知温度下的持久强度进行计算,得到可信的结果。
例如现在要计算温度925℃下的持久强度。首先观察在各标准时间下温度-应力散点图,仅以50、100、200小时为例,如图5,线形为曲线。在双对数坐标系下散点线形亦为曲线,如图6。因此用线性拟合方法是不恰当的。采用样条插值【3】方法进行插值,获得温度925℃各标准时间下应力值。其散点图见图7,双对数坐标系下散点图见图8,由线形形状知应用线性拟合法较好。回归方程为lgS=6.5870-0.1978*lgt(5)
得到对应持久强度曲线如图9。其相关性系数为-0.9923,以95%概率接受拟合结果。
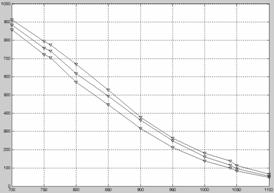
图5 50、100、200小时下温度-应力散点图
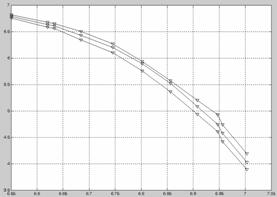
图6 双对数坐标系50、100、200小时下
温度-应力散点图
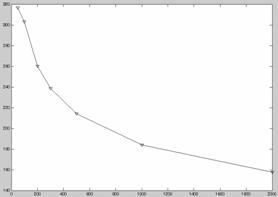
图7 925℃应力-寿命散点图
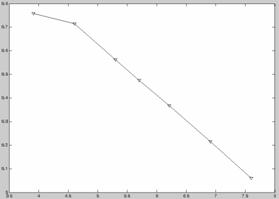
图8 双对数坐标系下925℃应力-寿命散点图
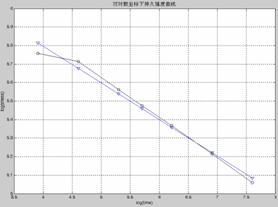
图9 双对数坐标系925℃应力-寿命拟合结果
与散点图相关性比较
2.3 给定温度、应力水平下持久时间预测
将方程(3)变形得:
 (6) (6)
在925℃下,例如给定应力S0=250MPa,则由(6)式算得t=218.9624 h, 可由以下公式计算 的95%的预测区间。 的95%的预测区间。
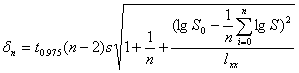
其中s为标准差,lxx为 离差平方和。则对此数据95%预测区间是(218.89,219.03)【2】。 离差平方和。则对此数据95%预测区间是(218.89,219.03)【2】。
3 结论
3.11由回归方程(2)得到的拟合曲线线性相关系数大于0.99,结合图(1),断定表(1)提供数据为拟合后给出的数据。相关系数未达到1的原因估计是取数据时舍入误差造成的。
3.12 2.2中样条插值适用于内插而不适用外插【3】。
3.13 应用最小二乘法对某种航空材料持久应力-寿命数据在双对数坐标系下进行线性拟合与实际符合良好,预测准确度高,可以在较少实验数据情况下预测材料的持久应力-寿命情况。
参考文献 (References)
[1]马逢时,何良才 等 [应用概率统计].1989年10月第1版. 高等教育出版社出版.
[2] D.Hanselman,B.littlefield[精通Matlab 6] 2002年6月第1版 清华大学出版社
[3]徐士良 [数值分析与算法].2006年1月第1版.机械工业出版社: |